19.
Что
понимается под внутригрупповой дисперсией для совокупности? Какова формула ее
расчета? Приведите пример. Что понимается под межгрупповой дисперсией
совокупности? Какова формула ее расчета? Приведите пример.
Внутригрупповая дисперсия (![]() ) свидетельствует о случайной вариации, которая не
зависит от признака, положенного в основу группировки.
) свидетельствует о случайной вариации, которая не
зависит от признака, положенного в основу группировки.
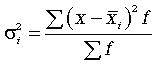 , где
, где
![]() - средняя
величина в группе
- средняя
величина в группе
Средняя
внутригрупповая дисперсия рассчитывается следующим образом: сначала
рассчитываются дисперсии по отдельным группам (![]() ), затем
рассчитывается средняя внутригрупповая дисперсия
), затем
рассчитывается средняя внутригрупповая дисперсия ![]() :
:
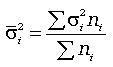
Межгрупповая дисперсия ![]() характеризует
систематическую вариацию, т.е. различия в величине исследуемого признака,
который положен в основу группировки. Эта дисперсия рассчитывается по формуле
характеризует
систематическую вариацию, т.е. различия в величине исследуемого признака,
который положен в основу группировки. Эта дисперсия рассчитывается по формуле
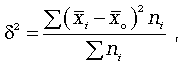 , где
, где
![]() - средняя
величина по отдельной группе
- средняя
величина по отдельной группе
ni - число единиц в группе
![]() - общая средняя арифметическая всей исследуемой совокупности.
- общая средняя арифметическая всей исследуемой совокупности.
Все
три вида дисперсии связаны между собой: общая дисперсия равна сумме средней
внутригрупповой дисперсии и межгрупповой дисперсии:
![]()
Данное
соотношение отражает закон, который называют правилом сложения дисперсий.
20.
Что
понимается под общей дисперсией совокупности? Какова формула ее расчета? Влияет
ли способ разделения на группы на значения общей дисперсии? Приведите пример.
Общая
дисперсия (![]() ) характеризует
вариацию признака всей совокупности под влиянием всех тех факторов, которые
обусловили данную вариацию. Эта величина определяется по формуле
) характеризует
вариацию признака всей совокупности под влиянием всех тех факторов, которые
обусловили данную вариацию. Эта величина определяется по формуле
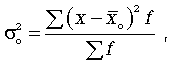 , где
, где
![]() общая средняя
арифметическая всей исследуемой совокупности.
общая средняя
арифметическая всей исследуемой совокупности.
С
другой стороны общая дисперсия равна сумме средней внутригрупповой дисперсии и
межгрупповой дисперсии:
![]()
Данное соотношение отражает закон, который называют правилом
сложения дисперсий.. Благодаря правилу
сложения дисперсий можно определить, какая часть общей дисперсии находится под
влиянием признака-фактора, положенного в основу группировки.
Чем
выше доля межгрупповой дисперсии ![]() в
общей дисперсии
в
общей дисперсии ![]() , тем
сильнее влияние факторного признака (разряда) на результативный
(выработку).
, тем
сильнее влияние факторного признака (разряда) на результативный
(выработку).
Эта доля характеризуется
эмпирическим коэффициентом детерминации:
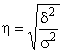
Для качественной оценки
тесноты связи между признаками пользуются соотношениями Чэддока.
|
|
0 |
0-0,2 |
0,2-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
1 |
|
Сила связи |
отсутствует |
очень слабая |
слабая |
умеренная |
заметная |
тесная |
весьма тесная |
функцио- нальная |
21.
Что
показывает коэффициент детерминации? Какова формула его расчета? В каких
единицах измеряется этот показатель? Каковы возможные значения этого
показателя? Что показывает эмпирическое корреляционное отношение? Какова
формула его расчета? В каких единицах измеряется этот показатель? Каковы
возможные значения этого показателя?
Эмпирический
коэффициент детерминации (![]() ) характеризует долю межгрупповой дисперсии в общей
дисперсии:
) характеризует долю межгрупповой дисперсии в общей
дисперсии:
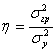 ,
принимает значения -1 до 1 и показывает, насколько вариация признака в
совокупности обусловлена фактором группировки.
,
принимает значения -1 до 1 и показывает, насколько вариация признака в
совокупности обусловлена фактором группировки.
![]() - межгрупповая дисперсия;
- межгрупповая дисперсия;
![]() - общая дисперсия.
- общая дисперсия.
Эмпирическое корреляционное отношение определяется по формуле:
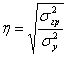 , принимает значения -1 до 1
, принимает значения -1 до 1
Пример
|
Группа |
Количество
заводов в группе, шт. |
Средняя
валовая продукция в сопоставимых ценах |
|
1 |
5 |
3,0 |
|
2 |
8 |
5,0 |
|
3 |
7 |
7,3 |
|
4 |
5 |
9,3 |
Определим
теперь среднее значение, общую дисперсию, и межгрупповую дисперсию валовой
продукции в сопоставимых ценах заводов:
 млн.
руб.;
млн.
руб.;
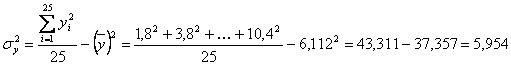 млн.
руб.2;
млн.
руб.2;
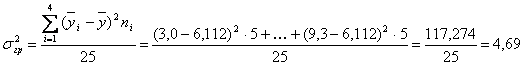 млн.
руб.2.
млн.
руб.2.
Коэффициент
детерминации будет равен:
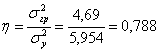
В
результате эмпирическое корреляционное отношение будет равно:

Рассчитанное
значение эмпирического корреляционного отношения свидетельствует о достаточно
высокой статистической связи между валовой продукцией в сопоставимых ценах и
среднегодовой стоимостью основных производственных фондов заводов.
22.
Как
рассчитывается статистика критерия в однофакторном дисперсионном анализе? Каков
закон ее распределения при справедливости основной гипотезы? Чем определяются
параметры этого закона? Как принимается решение в однофакторном дисперсионном
анализе по рассчитанному значению статистики критерия?
Задачей
дисперсионного анализа является изучение влияния одного или нескольких факторов
на рассматриваемый признак.
Однофакторный
дисперсионный анализ используется в тех случаях, когда есть в распоряжении три
или более независимые выборки, полученные из одной генеральной совокупности
путем изменения какого-либо независимого фактора, для которого по каким-либо
причинам нет количественных измерений.
В качестве критерия
необходимо воспользоваться критерием Фишера:
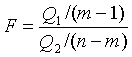 ., где
., где
Q 1 – сумма квадратов отклонений выборочных средних ![]() от общего среднего
от общего среднего ![]()
Q2 – сумма квадратов отклонений наблюдаемых значений ![]() от выборочной средней
от выборочной средней ![]()
Если расчетное значение
критерия Фишера будет меньше, чем табличное значение ![]() – нет оснований считать, что независимый фактор
оказывает влияние на разброс средних значений (т.е. гипотеза не подтвердилась). В противном случае, независимый
фактор оказывает существенное влияние на разброс средних значений (гипотеза справедлива).
– нет оснований считать, что независимый фактор
оказывает влияние на разброс средних значений (т.е. гипотеза не подтвердилась). В противном случае, независимый
фактор оказывает существенное влияние на разброс средних значений (гипотеза справедлива).
23-25.
Задачи статистики в изучении связи. Взаимосвязанные
признаки и их классификация.
Задачи статистики состоят в выявлении
связи, определении ее направления и ее измерении. Наиболее же общая задача –
это прогнозирование и регулирование социально-экономических явлений на основе
полученных представлений о связях между явлениями.
Статистика рассматривает экономический
закон как существенную и устойчивую связь между определенными явлениями и
процессами. Познавая связи, статистика познает законы. А их знание позволяет
управлять общественным развитием. Основой изучения связей является качественный
анализ.
Различают два вида признаков:
(1) Факторные –
те, которые влияют на изменение других процессов.
(2) Результативные –
те, которые изменяются под воздействием других признаков.
Виды и формы связей, различаемые в статистике.
В статистике связи классифицируются
по степени их тесноты. Исходя из этого
различают функциональную (полную) и статистическую (неполную,
корреляционную) связь.
Функциональная связь – такая связь, при которой значение
результативного признака целиком определяется значением факторного (например,
площадь круга). Она полностью сохраняет свою силу и проявляется во
всех случаях наблюдения и для всех единиц наблюдения. Каждому значению
факторного признака соответствует одно или несколько определенных значений
результативного признака.
Для корреляционной связи характерно
то, что одному и тому же значению факторного признака может соответствовать
сколько угодно различных значений результативного признака. Здесь связь
проявляется лишь при достаточно большом количестве наблюдений и лишь в форме
средней величины.
По направлению изменений
факторного и результативного признака различают связь прямую и обратную.
Прямая связь – такая связь, при которой с
изменением значений факторного признака в одну сторону, в ту же сторону
меняется и результативный признак.
Обратная связь – такая связь, при которой с
увеличением (уменьшением) факторного признака происходит уменьшение
(увеличение) результативного признака.
По аналитическому
выражению выделяются две основные формы связи:
– прямолинейная (выражается уравнением прямой);
– криволинейная (описывается уравнениями кривых
линий – гипербол, парабол, степенных функций).
Описательные
(механические) методы
К ним относятся: (1)
метод приведения параллельных рядов,
(2)
балансовый метод,
(3)
графический метод,
(4)
метод аналитической группировки.
Наибольший эффект достигается при
комбинировании нескольких методов.
(1) Метод приведения параллельных рядов
Приводится ряд данных по одному признаку и
параллельно с ним – по другому признаку, связь с которым предполагается. По
вариации признака в первом и втором ряду судят о наличии связи признаков. Такой
метод позволяет вывести только направление связи, но не измерить ее.
(2) Балансовый метод
Взаимосвязь может быть также
охарактеризована с помощью балансов.
(3) Графический метод
Может использоваться как самостоятельно,
так и совместно с другими методами.
Если конкретные данные перенести на
график, то полученное изображение называется полем корреляции. На оси абсцисс
откладывается значение факторного признака, а на оси ординат – результативного.
Каждая единица, обладающая определенным значением факторного и результативного
признака, обозначается точкой.
Беспорядочное расположение говорит об
отсутствии связи. Наоборот, чем сильнее связь, тем теснее точки группируются
вокруг определенной линии.
(4) Метод аналитической
группировки
Сначала выбираются два признака: факторный
и результативный. Пол факторному признаку производится
группировка, а по результативному – подсчет средних или относительных величин.
Путем сопоставления характера изменений
значений факторного и результативного признака можно сделать вывод о наличии
связи и ее направлении. При помощи метода аналитической группировки можно
сделать вывод и о тесноте связи.
Метод аналитической группировки
Метод аналитической группировки считается
одним из основных методов изучения связей между экономическими явлениями.
Процесс установления связей между экономическими явлениями начинается с
группировки единиц совокупности по факторному признаку. Затем приступают к
вычислению синтетических показателей (относительных и средних величин) для
результативного признака по группам, на которые была разбита совокупность.
Различие между результативными и
факторными признаками относительно: один и тот же признак в зависимости от
исследуемого явления может быть результативным или факторным. Например,
урожайность в зависимости от уровня агротехники является результативным
признаком, в то же время она является факторным признаком при изучении
себестоимости продукции.
В изучении массовых явлений хозяйственной
деятельности предприятий первостепенное значение имеет оценка общих итогов
деятельности, различий в достигнутых результатах по предприятиям и т. п.
Эту задачу решают аналитические группировки по результативному признаку. Они
позволяют установить различия в полученных результатах, отделить передовое от отстающего, оценить связь результатов с
комплексом факторов.
26.
Порядок вычислений:
1) Составить четырехпольную корреляционную
таблицу.
Образец
четырехпольной корреляционной таблицы
2) . Коэффициент ассоциации вычисляется по
следующей формуле:
где а, б, в, г - численности альтернативных признаков, расположенные в
клетках корреляционной "таблицы" (ни одна не должна быть меньше 5).
3) . На основании полученного результата
выявляем связь между изучаемыми признаками:
3.1)
Если коэффициент имеет положительный знак (+), то
связь положительная, и, наоборот, при отрицательном знаке (-) - связь
отрицательная.
3.2) По абсолютному значению коэффициента (от 0 до 1) оцениваем
количественную меру связи:
- если ![]() = 0 - корреляция отсутствует (данные
факторы между собой нейтральны);
= 0 - корреляция отсутствует (данные
факторы между собой нейтральны);
- если 0,09 ![]() 0,19 - статистическая взаимосвязь
очень слабая;
0,19 - статистическая взаимосвязь
очень слабая;
- если 0,2 ![]() 0,49 - статистическая взаимосвязь
слабая;
0,49 - статистическая взаимосвязь
слабая;
- если 0,5 ![]() 0,69 - статистическая взаимосвязь
средняя;
0,69 - статистическая взаимосвязь
средняя;
- если 0,70 ![]() 0,99 - статистическая взаимосвязь
сильная.
0,99 - статистическая взаимосвязь
сильная.
Т.о., на основании расчетного ![]() делается вывод о том, что между исследуемыми признаками
существует слабая (средняя, сильная) положительная (отрицательная) связь.
делается вывод о том, что между исследуемыми признаками
существует слабая (средняя, сильная) положительная (отрицательная) связь.
4)
Проверка достоверности выявленной связи осуществляется следующим
образом:
- по таблице 14 находится критический
коэффициент корреляции ![]() при
при ![]() < 0,05 и числе степеней свободы К =
N - 2,
< 0,05 и числе степеней свободы К =
N - 2,
- сравниваем полученные
результаты ![]() и
и ![]() .
.
Коэффициент ассоциации (coefficient of association) – оценка степени
тесноты связи между качественными признаками, каждый из которых представлен в
виде альтернативного признака. Однако в тех случаях, когда один из четырех
показателей отсутствует, величина коэффициента равна 1, что дает преувеличенную
оценку связи между признаками.
ВЫВОДЫ:
На основании того, что ![]() больше
больше
![]() , наличие
обнаруженной связи считается достоверным при
, наличие
обнаруженной связи считается достоверным при ![]() < 0,05.
< 0,05.
На основании того, что ![]() меньше
меньше
![]() , наличие обнаруженной связи считается недостоверным при
, наличие обнаруженной связи считается недостоверным при ![]() < 0,05.
< 0,05.
Этот
коэффициент используется в тех случаях, где, например,
необходимо исследовать тесноту зависимости между качественными признаками,
каждый из которых представлен в виде альтернативных признаков.
27-28.
Статистическая (стохастическая) связь — это такая связь между признаками, при которой для
каждого значения признака-фактора X признак-результат Y может в определенных пределах принимать любые
значения с некоторыми вероятностями; при этом его статистические (массовые)
характеристики (например, среднее значение) изменяются по определенному закону.
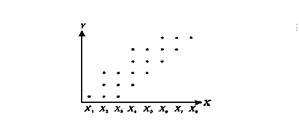
Детерминированная связь двух величин возможна лишь при условии, что вторая из них зависиттолько от первой и ни от чего более. Статическая связь не имеет ограничений и условий, присущих
детерминированной связи.
Таблица сопряженности - средство
представления совместного распределения двух переменных, предназначенное для
исследования связи между ними. Таблица сопряженности является наиболее универсальным средством
изучения статистических связей, так как в ней могут быть представлены
переменные с любым уровнем измерения.
Строки таблицы сопряженности соответствуют значениям одной
переменной, столбцы - значениям другой переменной (количественные шкалы
предварительно должны быть сгруппированы в интервалы). На пересечении строки и
столбца указывается частота совместного появления fij соответствующих значений двух
признаков xi и yj.
Сумма частот по строке fi называется маргинальной частотой
строки; сумма частот по столбцу fj - маргинальной частотой столбца. Сумма
маргинальных частот равна объему выборки n; их
распределение представляет собой одномерное распределение переменной,
образующей строки или столбцы таблицы.
Таблицы сопряженности используются для проверки гипотезы о наличии
связи между двумя признаками ( Статистическая связь, Критерий "хи-квадрат" ), а также для измерения тесноты связи
( Коэффициент фи, Коэффициент контингенции, Коэффициент Крамера)
29.
Что в статистике называется рядом
динамики? Что такое уровень ряда? Что понимается под моментыми
рядами динамики, интервальными? Приведите примеры.
Ряд динамики (или временной ряд) – это числовые значения определенного статистического
показателя в последовательные моменты или периоды времени (т.е. расположенные в
хронологическом порядке).
Числовые
значения того или иного статистического показателя, составляющего ряд динамики,
называют уровнями ряда и обычно обозначают буквой y.
Первый член ряда y1 называют начальным
или базисным уровнем, а последний yn
– конечным. Моменты или периоды времени, к которым относятся
уровни, обозначают через t.
Ряды
динамики, как правило, представляют в виде таблицы или графика, причем по оси
абсцисс строится шкала времени t,
а по оси ординат – шкала уровней ряда y.
Ряды
динамики классифицируются по следующим основным признакам:
По времени — ряды моментные и интервальные (периодные), которые показывают уровень явления на
конкретный момент времени или на определенный его период. Сумма уровней
интервального ряда дает вполне реальную статистическую величину за несколько
периодов времени, например, общий выпуск продукции, общее количество проданных
акций и т.п. Уровни моментного ряда, хотя и можно суммировать, но эта сумма
реального содержания, как правило, не имеет. Так, если сложить величины запасов
на начало каждого месяца квартала, то полученная сумма не означает квартальную
величину запасов.
30.
Сглаживание
временных рядов методом скользящего среднего. Запишите формулу расчёта значений
сглаженного временного ряда и поясните использованные обозначения.
Данный метод применяется
для характеристики
тенденции развития
исследуемой статистической совокупности и основан на
расчете
средних уровней ряда за
определенный период. Последовательность определения
скользящей средней:
- устанавливается интервал сглаживания
или число входящих в него
уровней. Если при расчете средней
учитываются три уровня, скользящая средняя
называется трехчленной,
пять уровней – пятичленной и т.д. Если сглаживаются
мелкие,
беспорядочные колебания уровней в ряду динамики, то интервал (число
скользящей средней)
увеличивают. Если волны следует сохранить, число членов
уменьшают.
- Исчисляют первый средний уровень по арифметической простой:
y1 = Sy1/m, где
y1 – I-ый уровень ряда;
m – членность скользящей средней.
- первый уровень отбрасывают, а в исчисление средней
включают уровень, следующий
за последним уровнем, участвующем в первом расчете.
Процесс продолжается до тех
пор, пока в расчет y будет включен последний
уровень исследуемого ряда
динамики yn.
- по ряду динамики, построенному из
средних уровней,
выявляют общую тенденцию
развития явления.
Отрицательной стороной
использования метода скользящей средней является
образование сдвигов в
колебаниях уровней ряда, обусловленных «скольжением»
интервалов укрупнения.
Сглаживание с помощью скользящей средней может
привести к появлению
«обратных» колебаний, когда выпуклая «волна» заменяется
на вогнутую.
31.
Сглаживание временных рядов методом
укрупнения интервалов. Отличие метода укрупнения интервалов от метода простого
скользящего среднего. Запишите формулу расчёта значений сглаженного ряда. Приведите пример.
K-ширина окна
Пример.
К=3
У1ср.=![]()
Далее по новым данным
строится новый график.
32.
33.
Сглаживание временных рядов
методом простого экспоненциального сглаживания.
При анализе временных рядов использовался
метод скользящей средней, в котором все данные независимо от периода их
возникновения являются равноправными. Существует другой способ, в котором данным приписываются веса,
более поздним данным придается больший вес, чем более ранним.
Метод экспоненциального сглаживания в отличие от метода скользящих
средних еще и может быть использован для краткосрочных прогнозов будущей
тенденции на один период вперед и автоматически корректирует любой прогноз в
свете различий между фактическим и спрогнозированным результатом. Именно
поэтому метод обладает явным преимуществом над ранее
рассмотренным.
Название метода происходит из того факта, что при его применении
получаются экспоненциально взвешенные скользящие
средние по всему временному ряду. При экспоненциальном
сглаживании учитываются все предшествующие наблюдения - предыдущее учитывается
с максимальным весом, предшествующее ему - с несколько меньшим, самое ранее
наблюдение влияет на результат с минимальным статистическим весом.
Алгоритм расчета экспоненциально сглаженных значений в любой точке
ряда i основан на трех величинах:
фактическое значение Ai в данной точке
ряда i,
прогноз в точке ряда Fi
некоторый заранее заданный коэффициент сглаживания W, постоянный по всему ряду.
Новый прогноз можно записать формулой:
![]()
Расчет экспоненциально сглаженных значений
При практическом использовании метода экспоненциального
сглаживания возникает две проблемы: выбор коэффициента сглаживания (W), который
в значительной степени влияет на результаты и определение начального условия (Fi). С одной стороны, для сглаживания случайных отклонений
величину нужно уменьшать. С другой стороны, для увеличения веса новых измерений
нужно увеличивать.
Хотя, в принципе, W может принимать любые значения из диапазона 0
< W < 1, обычно ограничиваются интервалом от 0,2 до 0,5. При высоких
значениях коэффициента сглаживания в большей степени учитываются мгновенные
текущие наблюдения отклика (для динамично развивающихся фирм) и, наоборот, при
низких его значениях сглаженная величина определяется в большей степени прошлой
тенденцией развития, нежели текущим состоянием отклика системы (в условиях
стабильного развития рынка).
Выбор коэффициента постоянной сглаживания
является субъективным.
Аналитики большинства фирм при обработке рядов используют свои традиционные
значения W. Так, по опубликованным данным в аналитическом отделе Kodak, традиционно используют значение 0,38, а на фирме Ford Motors – 0,28 или 0,3.
Ручной расчет экспоненциального сглаживания требует крайне
большого объема монотонной работы. На примере рассчитаем
прогнозный объем на 13 квартал, если имеются данные объема продаж за последние
12 кварталов, используя метод простого экспоненциального сглаживания.
Предположим, что на первый квартал прогноз продаж составил 3. И
пусть коэффициент сглаживания W =0,8.
Заполним в таблице третий столбец, подставляя для каждого
последующего квартала значение предыдущего по формуле:
Для 2 квартала F2 =0,8*4 (1-0,8)*3 =3,8
Для 3 квартала F3 =0,8*6 (1-0,8)*3,8 =5,6
Аналогично, рассчитывается сглаженное значение для коэффициента
0,5 и 0,33.
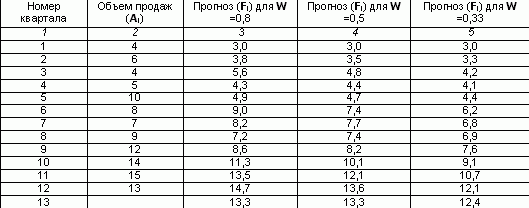
Расчет прогноза объема продаж
34.
Аналитическое выравнивание
временного ряда
Основным
способом моделирования и изучения таким образом
основной тенденции временного ряда (ряда динамики) является аналитическое
выравнивание временного ряда. При этом строится аналитическая функция,
характеризующая зависимость уровней ряда динамики от времени. Эта функция также
называется трендом. Сам такой способ выявления основной тенденции называется
аналитическим выравниванием. В качестве основной тенденции выдвигается гипотеза
о некоторой аналитической функции, выражающей данную зависимость. Для
определения (оценивания) параметров тренда обычно используется метод наименьших
квадратов:
Пусть общее количество точек равно n.
Отклонение i-й точки от
искомой прямой:
![]()
Отклонения могут быть как положительными,
так и отрицательными. Поэтому для того, чтобы определить близость искомой
функции к табличным точкам, необходимо составить сумму квадратов всех отклонений.
Метод
наименьших квадратов заключается в минимизации
суммы квадратов отклонений. В нашем случае эта функция равна
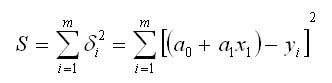
Для нахождения минимума функции S необходимо приравнять нулю ее
частные производные. В результате получим систему уравнений:
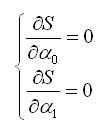
Опуская промежуточные преобразования, получим систему уравнений
для нахождения неизвестных коэффициентов:
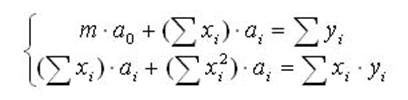
Здесь m - количество точек; суммирование
здесь и далее предполагается по всем точкам. Метод наименьших квадратов несложно
распространить на общий случай, когда мы будем искать функцию ф(х) в виде полинома степени n:
![]()
35.
Средний уровень ряда.
Средний
уровень ряда определяет
обобщенную величину абсолютных уровней. Он определяется по средней,
исчисленной из значений, меняющихся во времени. Методы расчета среднего уровня
интервального и моментного рядов динамики разные.
Средний уровень из абсолютных уровней для
интервальных рядов динамики рассчитывается по формуле средней арифметической:
1. При равных интервалах используют среднюю арифметическую простую:
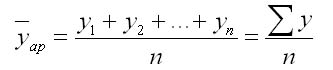
где у — абсолютные уровни ряда;
n — число уровней ряда.
2. При неравных интервалах используют среднюю арифметическую взвешенную:
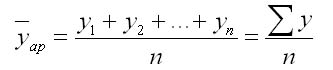
где у1,...,уn —
уровни ряда динамики;
t1,... tn — веса,
длительность интервалов времени.
Средний
уровень моментного ряда динамики
рассчитывается по формуле:
1. С равностоящими уровнями рассчитывается по
формуле средней хронологической моментного ряда:

где у1,...,уn —
уровни периода, за который делается расчет;
n — число уровней;
n-1 — длительность периода времени.
2. С неравностоящими
уровнями рассчитывается по формуле средней хронологической взвешенной:
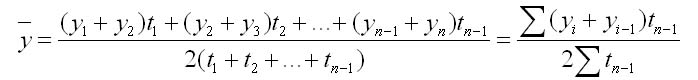
где у1,...,уn —
уровни рядов динамики;
t — интервал времени между смежными уровнями
Средний абсолютный прирост в
задачах статистики
Средний
абсолютный прирост определяется
как среднее из абсолютных приростов за равные промежутки времени одного
периода. Он рассчитывается по формулам: 1. По цепным данным об абсолютных
приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую:
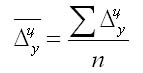
где n — число степенных абсолютных
приростов в исследуемом периоде.
2. Средний
абсолютный прирост рассчитывают через базисный абсолютный прирост в случае
равных интервалов
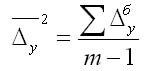
где m — число уровней ряда динамики в
исследуемом периоде, включая базисный.
Средний темп роста
Средний
темп роста есть
свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает,
во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
В качестве основы и критерия правильности
вычисления среднего темпа роста (снижения) применяется обобщающий показатель,
который рассчитывается как произведение цепных темпов роста, равное темпу роста
за весь рассматриваемый период. Если значение признака образуется как
произведение отдельных вариантов, то используют среднюю
геометрическую.
Так как средний темп роста представляет собой
средний коэффициент роста, выражен в процентах, то для равностоящих рядов
динамики расчеты по средней геометрической сводятся к вычислению средних
коэффициентов роста из цепных по «цепному способу»:
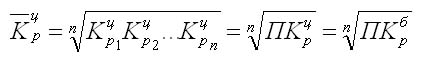
где n — число цепных коэффициентов
роста;
Кц — цепные коэффициенты роста;
Кб — базисный коэффициент роста за весь период.
Определение среднего коэффициента роста может
быть упрощено, если будут ясны уровни динамического ряда. Так как произведение
цепных коэффициентов роста равно базисному, то в
подкоренное выражение подставляют базисный коэффициент роста.
Формула для определения среднего коэффициента роста для
равностоящих рядов динамики по «базисному способу» будет такая:
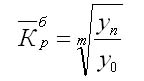
36.
Какие Вам известны абсолютные показатели
изменения уровня ряда?
Все эти показатели могут определяться базисным
способом, когда уровень данного периода сравнивается с первым (базисным)
периодом, либо цепным способом – когда сравниваются два уровня соседних
периодов.
Напишите
формулы расчета.
Базисное абсолютное изменение представляет собой
разность конкретного и первого уровней ряда, определяется по формуле
![]()
Оно показывает, на сколько (в
единицах показателей ряда) уровень одного (i-того) периода больше или меньше
первого (базисного) уровня, и, следовательно, может иметь знак «+» (при
увеличении уровней) или «–» (при уменьшении уровней).
Цепное абсолютное изменение представляет собой
разность конкретного и предыдущего уровней ряда, определяется по формуле
![]()
Оно показывает, на сколько (в единицах показателей
ряда) уровень одного (i-того) периода больше или меньше предыдущего уровня, и
может иметь знак «+» или «–».
Поясните,
как зависит способ расчета от выбора базы сравнения.
Какие Вам
известны относительные показатели изменения уровня ряда? Напишите формулы
расчета.
Базисное относительное изменение (базисный темп роста
или базисный индекс динамики) представляет собой соотношение конкретного и
первого уровней ряда, определяясь по формуле
![]()
Цепное относительное изменение (цепной темп роста или
цепной индекс динамики) представляет собой соотношение конкретного и
предыдущего уровней ряда, определяясь по формуле
![]()
Поясните, как
зависит способ расчета от выбора базы сравнения.
Относительное изменение показывает во сколько раз
уровень данного периода больше уровня какого-либо предшествующего периода (при i>1) или какую его часть составляет (при i<1). Относительное изменение может выражаться в виде
коэффициентов, то есть простого кратного отношения (если база сравнения принимается за единицу),
и в процентах (если база сравнения принимается за 100 единиц) путем домножения относительного изменения на 100%.
37.
Какие Вам
известны средние показатели изменения уровня ряда? Напишите формулы расчета
среднего абсолютного прироста, темпа роста и темпа прироста уровней ряда.
Средний абсолютный прирост определяется как среднее из
абсолютных приростов за равные промежутки времени одного периода. Он
рассчитывается по формулам: 1. По цепным данным об абсолютных приростах за ряд
лет рассчитывают средний абсолютный прирост как среднюю
арифметическую простую:
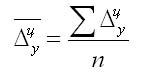
где n — число степенных абсолютных приростов в исследуемом
периоде.
2. Средний абсолютный
прирост рассчитывают через базисный абсолютный прирост в случае
равных интервалов
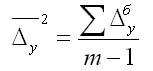
где m — число уровней ряда динамики в исследуемом периоде,
включая базисный.
Средний темп роста есть свободная обобщающая
характеристика интенсивности изменения уровней ряда динамики
и показывает, во сколько раз в среднем за единицу времени изменяется уровень
ряда динамики.
В качестве
основы и критерия правильности вычисления среднего темпа роста (снижения)
применяется обобщающий показатель, который рассчитывается как произведение
цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если
значение признака образуется как произведение отдельных вариантов, то
используют среднюю геометрическую.
Так как средний
темп роста представляет собой средний коэффициент роста, выражен в процентах,
то для равностоящих рядов динамики расчеты по средней геометрической сводятся к
вычислению средних коэффициентов роста из цепных по
«цепному способу»:
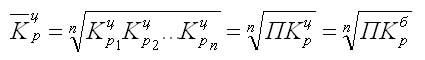
где n — число цепных коэффициентов роста;
Кц — цепные коэффициенты роста;
Кб — базисный
коэффициент роста за весь период.
Темп изменения (темп прироста) уровней – относительный
показатель, показывающий, на сколько процентов данный уровень больше (или
меньше) другого, принимаемого за базу сравнения. Он рассчитывается путем
вычитания из относительного изменения 100%, то есть по формуле:
![]() ,
,
или как
процентное отношение абсолютного изменения к тому уровню, по сравнению с
которым рассчитано абсолютное изменение (базисный уровень), то есть по формуле:
![]() .
.
Каким недостатком
обладают эти показатели? В каких случаях целесообразно их использование? Как
указанные недостатки могут быть устранены? Напишите формулы расчёта средних
показателей, обеспечивающих сохранение суммарного значения ряда.
38.
Как по
значениям показателей изменения уровней ряда определить вид основной тенденции?
Приведите примеры.
Выявление
общей тенденции ряда динамики можно произвести путем сглаживания ряда динамики
с помощью метода скользящей средней. Сущность этого приема состоит в том, что
по исходным уровням ряда (эмпирическим данным) определяют расчетные
(теоретические) уровни.
Основное
условие применения этого метода состоит в вычислении звеньев подвижной
(скользящей) средней из такого числа уровней ряда, которое соответствует
длительности наблюдаемых в ряду динамики циклов.
![\includegraphics[width=6.54in,height=1.69in]{D:/html/work/link1/metod/met90/met9039.eps}](stat.files/image109.jpg)
![\includegraphics[width=3.28in,height=0.65in]{D:/html/work/link1/metod/met90/met9040.eps}](stat.files/image111.jpg) ,
,