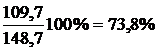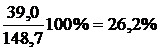Вопросы зачета по курсу "Статистика"

Общие понятия статистики. Статистическое наблюдение. Выборочный метод в статистическом наблюдении.

1. Что такое массовое явление? Каковы его свойства? Приведите примеры. Что называется статистической совокупностью? Что понимается под единицей статистической совокупности? Приведите примеры. Что в статистике понимается под признаком единицы совокупности? Что понимается под статистическим признаком? Что такое вариация признака? Какие признаки различают в статистике? Приведите примеры. Что называется статистической закономерностью? Какие необходимы условия для ее выявления? В чем состоит сущность закона больших чисел?

2. Что в статистике понимается под статистическим наблюдением? Какие требования предъявляются к статистическим данным? Какие Вам известны формы статистического наблюдения? Какие особенности каждой формы статистического наблюдения Вам известны?

3. Какие виды статистического наблюдения выделяют по охвату единиц совокупности? Поясните на примере. Какие виды статистического наблюдения выделяют по времени регистрации фактов? Поясните на примере. Какие виды статистического наблюдения выделяют по источникам получения информации? Поясните на примере.

4. Как можно классифицировать ошибки статистического наблюдения? Каковы причины возникновения каждого вида ошибки? Как измеряются ошибки репрезентативности? Какие данные требуются для расчета этих ошибок? Что такое коэффициент доверия t? Приведите пример вычисления ошибок репрезентативности. Как можно оценить требуемый объем выборки, по известным значениям ошибок репрезентативности? Поясните на примере.

Обобщающие статистические показатели

5. Какие основные виды обобщающих статистических показателей Вам известны? Какие единицы измерения используются в каждом виде? Что такое абсолютные статистические показатели? Поясните на примере.

6. Что представляет собой относительный статистический показатель? Какие единицы измерения используются для представления относительного статистического показателя? Каковы формулы расчета относительных показателей динамики, плана и реализации плана? Какова взаимосвязь между этими показателями? Поясните на примере.

7. Что представляет собой относительный статистический показатель? Какие единицы измерения используются для представления относительного статистического показателя? Каковы формулы расчета относительных показателей структуры, интенсивности, сравнения, уровня экономического развития?

8. Какие виды средних величин применяются в статистике? Какой общей формулой можно представить все виды среднего, среднего взвешенного? Поясните все используемые обозначения. Что понимается под взвешиванием? Приведите примеры. В чем состоит правило мажорантности средних?

9. Какова формула расчета среднего арифметического? Какова формула расчета среднего арифметического взвешенного? Какие свойства среднего арифметического Вам известны? Где применяется среднее арифметическое? Приведите пример.

10. Какова формула расчета среднего геометрического? Какова формула расчета среднего геометрического взвешенного? Где применяется среднее геометрическое? Приведите пример.

11. Какова формула расчета среднего гармонического? Какова формула расчета среднего гармонического взвешенного? Где применяется среднее гармоническое? Приведите пример.

12. Какова формула расчета среднего квадратического? Какова формула расчета среднего квадратического взвешенного? Где применяется среднее квадратическое? Приведите пример.

Показатели вариации и однофакторный дисперсионный анализ

13. Перечислите показатели вариации, которые применяются в статистике. Какие свойства выборки (амплитуда колебаний, степень колеблемости относительно средней, однородность) показывают каждый из них?

14. Как рассчитывается размах вариации признака? В чем измеряется этот показатель? Какие свойства выборки (амплитуда колебаний, степень колеблемости относительно средней, однородность) показывает этот показатель? Приведите пример.

15. Как рассчитывается среднее линейное отклонение признака (простое и взвешенное)? В чем измеряется этот показатель? Какие свойства выборки (амплитуда колебаний, степень колеблемости относительно средней, однородность) показывает этот показатель? Приведите пример.

16. Как рассчитывается дисперсия признака (простое и взвешенное)? В чем измеряется этот показатель? Какие свойства выборки (амплитуда колебаний, степень колеблемости относительно средней, однородность) показывает этот показатель? Приведите пример.

17. Как рассчитывается среднеквадратичное отклонение признака (простое и взвешенное)? В чем измеряется этот показатель? Какие свойства выборки (амплитуда колебаний, степень колеблемости относительно средней, однородность) показывает этот показатель? Приведите пример.

18. Как рассчитывается показатель вариации (линейный и нелинейный)? В чем измеряется этот показатель? Какие свойства выборки (амплитуда колебаний, степень колеблемости относительно средней, однородность) показывает этот показатель? Приведите пример.

19. Что понимается под внутригрупповой дисперсией для совокупности? Какова формула ее расчета? Приведите пример. Что понимается под межгрупповой дисперсией совокупности? Какова формула ее расчета? Приведите пример.

20. Что понимается под общей дисперсией совокупности? Какова формула ее расчета? Влияет ли способ разделения на группы на значения общей дисперсии? Приведите пример.

21. Что показывает коэффициент детерминации? Какова формула его расчета? В каких единицах измеряется этот показатель? Каковы возможные значения этого показателя? Что показывает эмпирическое корреляционное отношение? Какова формула его расчета? В каких единицах измеряется этот показатель? Каковы возможные значения этого показателя?

22. Как рассчитывается статистика критерия в однофакторном дисперсионном анализе? Каков закон ее распределения при справедливости основной гипотезы? Чем определяются параметры этого закона? Как принимается решение в однофакторном дисперсионном анализе по рассчитанному значению статистики критерия?

Анализ статистических взаимосвязей

23. Понятие факторного и результативного признака. Какие виды связей могут наблюдаться между факторным и результативным признаками? Приведите известные Вам меры оценки связи между двумя количественными признаками.

24. Понятие факторного и результативного признака. Какие виды связей могут наблюдаться между факторным и результативным признаками? Приведите известные Вам меры оценки связи между количественным результативным и качественным факторными признаками. Что означает значимость статистической связи? Как осуществляется проверка значимости связи между этими признаками?

25. Понятие факторного и результативного признака. Какие виды связей могут наблюдаться между факторным и результативным признаками? Приведите известные Вам меры оценки связи между двумя качественным признаками.

26. Как рассчитывается коэффициент ассоциации? Что показывает этот коэффициент? Какие выводы можно сделать исходя из рассчитанных значений коэффициента ассоциации? В каких случаях возможно использование этого коэффициента? Приведите пример.

27. Что означает наличие статистической связи между двумя качественными признаками. В чём отличие статистической связи от детерминированной? Что называется таблицей сопряжённости? Объясните способ её построения. Как и для чего используется таблица сопряжённости?

28. Что означает наличие статистической связи между двумя качественными признаками? В чём отличие статистической связи от детерминированной? Как осуществляется проверка значимости статистической связи между двумя качественными признаками с использованием таблицы сопряжённости? Сформулируйте основную гипотезу и способ её проверки.

Анализ рядов динамики

29. Что в статистике называется рядом динамики? Что такое уровень ряда? Что понимается под моментыми рядами динамики, интервальными? Приведите примеры.

30. Сглаживание временных рядов методом скользящего среднего. Запишите формулу расчёта значений сглаженного временного ряда и поясните использованные обозначения.

31. Сглаживание временных рядов методом укрупнения интервалов. Отличие метода укрупнения интервалов от метода простого скользящего среднего. Запишите формулу расчёта значений сглаженного ряда. Приведите пример.

32. Устранение грубых сбоев измерений методом скользящей медианы. Каким параметром характеризуется медианный фильтр? Как влияет этот параметр на вид сглаженного ряда? Какие положительные и отрицательные свойства этого метода Вам известны? Запишите формулу расчёта значений сглаженного ряда. Приведите пример.

33. Сглаживание временных рядов методом простого экспоненциального сглаживания. Запишите формулу расчёта значений сглаженного ряда. Чему равно значение начального уровня сглаженного ряда? Каким параметром характеризуется метод? Как от значений этого параметра зависит результат обработки ряда? Каковы максимальное и минимальное значения параметра? Какой будет наблюдаться результат обработки ряда, если задать минимальное значение параметра, максимальное значение?

34. Аналитическое выравнивание временного ряда. Постановка задачи. В чём состоит метод наименьших квадратов? Как с помощью метода наименьших квадратов рассчитываются коэффициенты линейного тренда?

35. Какие Вам известны средние показатели уровней ряда? Напишите формулы расчета среднего уровня ряда. Поясните на примере, в каких случаях эти формулы применяются.

36. Какие Вам известны абсолютные показатели изменения уровня ряда? Напишите формулы расчета. Поясните, как зависит способ расчета от выбора базы сравнения. Какие Вам известны относительные показатели изменения уровня ряда? Напишите формулы расчета. Поясните, как зависит способ расчета от выбора базы сравнения.

37. Какие Вам известны средние показатели изменения уровня ряда? Напишите формулы расчета среднего абсолютного прироста, темпа роста и темпа прироста уровней ряда. Каким недостатком обладают эти показатели? В каких случаях целесообразно их использование? Как указанные недостатки могут быть устранены? Напишите формулы расчёта средних показателей, обеспечивающих сохранение суммарного значения ряда.

38. Абсолютные и относительные показатели изменения уровней ряда. Как по значениям показателей изменения уровней ряда определить вид основной тенденции? Приведите примеры.

1.

а)Массовое явление- предмет статистической науки.

В настоящее время содержание статистической науки определяется следующим образом:

статистика как общественная наука изучает закономерности количественных отношений массовых общественных явлений, рассматриваемых в непосредственной связи с их качественным содержанием.

В определении подчеркнуто три момента:

1. Статистика имеет дело с количеством, то есть с величинами явлений.

2. Она рассматривает количество в связи с качеством явлений и процессов в конкретных условиях места и времени.

3. Статистика изучает не отдельные, а массовые явления.

В массовом явлении участвует множество элементов, существенные свойства которых схожи. Наличие какого-либо свойства у отдельного элемента является случайностью. Однако, при объединении большого числа элементов в единое целое общее действие дает результат, практически независимый от случая.

б) Объект статистического исследования называют статистической совокупностью.

Статистическая совокупность – это множество единиц, которые обладают массовостью, однородностью, определенной целостностью, взаимозавис. Отдельных единиц.

Единица совокупности — каждая конкретная единица статистической совокупности.

Одна и таже статистическая совокупность может быть однородна по одному признаку и неоднородна по другому.

Пример: Единицы совокупности характеризуются общими свойствами, которые наз – ся признаки, под которыми понимают: например, имея множество коммерческих банков, наряду с качественной определенностью, т.е. принадлежностью к кредитным учреждениям, существуют различия по размеру уставных фондов, суммам активов и т.д..

Признаки ед.стат.совокупности.

признаки отбирают с учетом целей исследования, возможностей их обработки и анализа полученных данных;
отобранных признаков не должно быть много;
признаки необходимо комбинировать, чтобы они взаимодополняли друг друга;
отобранные признаки должны учитывать возможности исследователя.

в) Статистический признак – это конкретное свойство, качество, отличительная черта единицы наблюдения.

Вариация признака — количественное изменение признака (для количественного признака) при переходе от одной единицы совокупности к другой.

Признак - это свойство, характерная черта или иная особенность единиц, объектов и явлений, которая может быть наблюдаема или измерена. Признаки делятся на количественные и качественные. Многообразие и изменчивость величины признака у отдельных единиц совокупности называется вариацией.

Атрибутивные (качественные) признаки не поддаются числовому выражению (состав населения по полу).

Количественные признаки имеют числовое выражение (состав населения по возрасту).

- дискретные( принимают целочисленные значения)например, количество единиц оборудования, количество рабочих.

- непрерывные(принимают вещественные значения)например, вес, стоимость продукции.

г) Закономерности, в которых необходимость неразрывно связана в каждом отдельном явлении со случайностью и лишь во множестве явлений проявляет себя как некий общий закон , называется статистическими.

Статистическая закономерность возникает как результат взаимодействия большого числа элементов, составляющих совокупность и характеризуют не столько поведение отдельного элемента совокупности, сколько всю совокупность в целом. Проявляющаяся в статистических закономерностях "необходимость" возникает вследствие взаимной компенсации и уравновешивания множества случайных факторов, "пробивает" себе дорогу через массу случайноcтей, контрпримеров, отступлений от нее.

ЗАКОН БОЛЬШИХ ЧИСЕЛ – общий принцип, в силу которого совместное действие случайных факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая. Первым примером действия этого принципа может служить сближение частоты наступления случайного события с его вероятностью при возрастании числа испытаний (часто использующееся на практике, например, при использовании частоты встречаемости какого-либо качества респондента в выборке как выборочной оценки соответствующей вероятности).

Сущность закона больших чисел состоит в том , что при большом числе независимых опытов частота появления какого-то события близка к его вероятности.

2.

Статистическое наблюдение является начальной (первой) стадией всякого статистического исследования.
Статистическим наблюдением называется планомерный научно обоснованный сбор данных или сведений о социально-экономических явлениях и процессах.
Не всякий сбор сведений является статистическим наблюдением.

статистическое наблюдение должно быть планомерным, массовым и систематическим.
Планомерность статистического наблюдения заключается в том, что оно готовится и проводится по разработанному плану, который включает вопросы методологии, организации, техники сбора информации, контроля за качеством собранного материала, его достоверности, оформления итоговых результатов.
Массовый характер статистического наблюдения предполагает, что оно охватывает большое число случаев проявления данного процесса, достаточное для того, чтобы получить правдивые статистические данные, характеризующие не только отдельные единицы, но и всю совокупность в целом.
Систематичность статистического исследования определяется тем, что оно должно проводиться либо систематически, либо непрерывно, либо регулярно.
Таким образом, к статистическому наблюдению предъявляются следующие требования:

полноты статистических данных (полноты охвата единиц изучаемой совокупности, сторон того или иного явления, а также полноты охвата во времени);
достоверности и точности данных;
их единообразия и сопоставимости.

Все многообразие форм, видов и способов наблюдения можно представить следующим образом.

По форме организации статистического наблюдения: отчетность; специально организованное статистическое обследование - перепись; регистры.

По видам статистического наблюдения:

а) по времени регистрации фактов (текущее или непрерывное; прерывное - периодическое, единовременное);

б) по охвату единиц совокупности (сплошное; несплошное - основного массива, выборочное, монографическое).

Основной формой статистического наблюдения является отчетность. Если первичный учет (первичный учетный документ) регистрирует различные факты, то отчетность является обобщением первичного учета.

Формой непрерывного статистического наблюдения является регистровое наблюдение (регистр), объектами которого являются долговременные процессы, имеющие фиксированное начало, стадию развития и фиксированное время завершения. Регистр основан на системе отслеживания состояния переменных и постоянных показателей

3.

а) По охвату единиц совокупности статистическое наблюдение бывает сплошным и несплошным.

Сплошное наблюдение охватывает все единицы исследуемой совокупности (например, общая перепись населения).

В свою очередь, несплошное наблюдение охватывает только часть исследуемой совокупности. В зависимости от того, как выбрана эта часть, несплошное наблюдение можно подразделить на выборочное (основано на принципе случайного отбора), метод основного массива (исследуются самые существенные или наиболее крупные единицы изучаемой совокупности) и так называемое монографическое наблюдение (подробное исследование отдельных единиц изучаемой совокупности с целью выявления намечающихся тенденций).

б) Рассмотрим коротко виды статистического наблюдения по времени регистрации фактов. Непрерывное (текущее) статистическое наблюдение - это систематическая регистрация фактов или явлений по мере их поступления с целью изучения их динамики. Например, регистрации актов гражданского состояния (рождения, браки, смерти), регистрация страховыми компаниями всех несчастных случаев и других неблагоприятных событий по мере их возникновения.

Видами прерывного наблюдения являются единовременное и периодическое. Первое есть разовое сплошное наблюдение для сбора количественных характеристик явления или процесса в момент его исследования. Периодическое наблюдение проводится через определенные промежутки времени по схожим программе и инструментарию. Например, периодическое исследование пассажиропотоков в общественном транспорте, периодическая регистрация цен производителей по отдельным товарам (один раз в месяц или в квартал).

Что касается способов получения статистической информации (способов статистического наблюдения), то здесь выделяют три основных способа: непосредственное наблюдение, документальное наблюдение и опрос.

Достаточно надежным источником данных является непосредственное наблюдение, когда можно установить факт, подлежащий регистрации. Но данный способ требует значительных затрат труда и наличия всех необходимых условий. Чаще всего он используется при наблюдении за вводом в действие строительных объектов.

Другой надежный способ - документальный, основанный на использовании в качестве источника информации различных документов учетного характера (счета, рекламации и т.д.) и способствующий получению точной информации.

Способ наблюдения, при котором источником сведений являются слова респондентов, называют опросом. Его разновидности: устный (экспедиционный), анкетный, корреспондентский, явочный опрос и саморегистрация.

Устный опрос может быть как прямым (непосредственное общение счетчика с респондентом), так опосредованным (например, по телефону).

При анкетном способе определенное число респондентов получают специальные вопросники либо лично, либо через средства печати. Данный вид опроса применяется в исследованиях, где нужны ориентировочные результаты, не претендующие на высокую точность (изучение общественного мнения).

Явочный способ используется в сплошном наблюдении, когда необходимо личное присутствие (регистрация браков, разводов, рождений и т.д.).

При корреспондентском способе сведения сообщаются штатом добровольных корреспондентов, в силу чего полученный материал не всегда носит качественный характер.

Наконец, при способе саморегистрации формуляры заполняются самими респондентами, а счетчики консультируют и собирают формуляры. В статистической практике различные виды статистических наблюдений могут сочетаться, дополняя друг друга.

4.

5.

6.

7.

Что представляет собой относительный статистический показатель?

Ответ

Относительный показатель в статистике – это обобщающая величина, которая дает числовую меру соотношения двух сопоставляемых числовых мер абсолютных показателей. Так как многие абсолютные величины взаимосвязаны, то и относительные величины одного типа в ряде случаев могут определяться через относительные величины другого типа. Основное условие правильного расчета относительной величины – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Таким образом, по способу получения относительные показатели – всегда величины производные, представляющие собой частное от деления двух абсолютных величин и характеризующие количественное соотношение между ними.

Одним из условий правильного использования статистических показателей является изучение абсолютных и относительных величин в их единстве. Если это условие не соблюдено, можно прийти к неправильному выводу. Только комплексное изучение абсолютных и относительных величин дает всестороннюю характеристику изучаемого явления. Существуют правила построения относительных статистических показателей:

1. Сравниваемые в относительном показателе абсолютные величины должны быть объективно связаны в реальной жизни, независимо от нашего желания (как соответствие смысловое, так и соответствие общее – частное).

2. При построении относительного статистического показателя сравниваемые исходные величины могут различаться только одним атрибутом, а именно:

· видом признака (при одинаковом объекте, периоде времени, договорном или фактическом характере показателей);

· временем (при том же признаке, объекте и т.п.);

· только фактическим, договорным или нормативным характером показателей (тот же объект, признак, время и т.п.).

Нельзя сопоставлять показатели по двум и более атрибутам.

Какие единицы измерения используются для представления относительного статистического показателя?

Ответ

Необходимо знать возможные границы существования относительного показателя. Например, относительные показатели вариации теряют смысл и не могут применяться, когда их знаменатели – средние значения признаков – близки к нулю, потому что при стремлении знаменателя к нулю относительный показатель стремится к абсурдному бесконечному значению. Аналогично, если исходные показатели в текущем и базисном периоде имеют разные знаки, то теряет смысл и не может применяться такая относительная величина динамики, как темп роста.

Например, если в первом полугодии предприятие имело убыток 100 тыс руб., а во втором получило прибыль 200 тыс. руб., то неверными будут рассуждения, что «экономический результат вырос вдвое» или «вырос в минус два раза».

Относительные показатели, измеряющие степень приближения некоторого признака к предельному значению, должны строиться так, чтобы в пределе увеличения они стремились к единице, а в пределе своего уменьшения – к нулю (например, использование абсолютного отклонения в числителе и нормы в знаменателе). Так строятся коэффициенты, измеряющие тесноту связи признаков, степень эффективности использования ресурсов. С использованием этих приемов обычно синтезируются относительные показатели экономической, социальной и экологической эффективности производственных процессов.

Каковы формулы расчета относительных показателей структуры, интенсивности, сравнения, уровня экономического развития?

Ответ

Как правило, относительные величины выражаются в процентах (база – 100%):

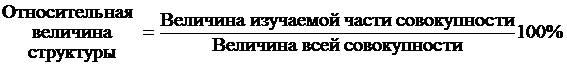Например:

Структура городского населения

Структура сельского населения

Относительные величины структуры дают возможность изучить структуру сбыта по ассортименту, состав работников предприятия по различным признакам (полу, возрасту, стажу), состав издержек и т.п.

В общем случае относительная величина подобного типа сравнивает фактический и базисный уровни. Кроме того, расчет относительной величины выполнения договорных обязательств может выполняться по методу нарастающего итога.

Относительные величины интенсивности

Эти величины показывают, насколько широко распространено изучаемое явление в той или иной среде. Они характеризуют соотношение разноименных, но связанных между собой абсолютных величин. В отличие от других видов относительных величин, относительные величины интенсивности всегда выражаются именованными величинами.

Рассчитываются относительные величины интенсивности делением абсолютной величины изучаемого явления на абсолютную величину, характеризующую объем среды, в которой происходит развитие или распространение явления. Относительная величина показывает, сколько единиц совокупности приходится на единицу другой совокупности. Например, стоимость имущества предприятия (акционерного общества), приходящаяся на одну акцию, получается делением восстановительной стоимости всего имущества на общее количество акций одного номинала.

Разновидностью относительных величин интенсивности являются относительные уровни социально-экономического развития, характеризующие уровни валового внутреннего продукта (ВВП), валового национального продукта (ВНП) и других показателей на душу населения.

Относительные величины сравнения

Относительные величины сравнения характеризуют количественное соотношение одноименных показателей, относящихся к различным объектам статистического наблюдения, и представляют собой частное от деления абсолютных статистических величин, которые могут относиться к одному и тому же периоду или моменту времени, но к различным объектам и территориям. Относительные величины сравнения используются для сопоставления уровня цен (или себестоимости) на один и тот же товар, реализуемый данным предприятием и другими предприятиями. В этом случае за базу для сравнения принимается цена (себестоимость) продукции данного предприятия (при одинаковой методике счета).

При расчете относительных величин сравнения необходимо обеспечить сопоставимость сравниваемых показателей, поскольку методы исчисления ряда показателей в разных странах или в разные периоды (моменты) времени неодинаковы. Сопоставимость показателей обеспечивается, в частности, учетом зависимости стоимости денежной единицы от времени, связью между показателями, относящимися к различным периодам и моментам времени, и т.п. Поэтому, прежде чем рассчитывать относительные показатели сравнения, необходимо обеспечить их пересчет к сопоставимому виду по единой методике.

8.

Какие виды средних величин применяются в статистике?

Ответ

Средняя величина - это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.

Существует 2 класса средних величин: степенные и структурные.

К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.

К степенным средним относятся средняя арифметическая, средняя гармоническая, средняя хронологическая, средняя геометрическая, средняя квадратическая, средняя кубическая.

Средняя величина всегда обобщает количественную вариацию признака, т. е. в средних величинах погашаются индивидуальные различия признака у отдельных единиц совокупности, обусловленные случайными обстоятельствами. Средняя величина позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям.

Какой общей формулой можно представить все виды среднего, среднего взвешенного?

Поясните все используемые обозначения. Что понимается под взвешиванием? Приведите примеры

Ответ

Степенные средние могут быть простыми и взвешенными.

Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:

Общая формула простой степенной средней величины

Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:

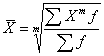
где X – значения отдельных статистических величин или середин группировочных интервалов;
m - показатель степени, от значения которого зависят следующие виды степенных средних величин:
при m = -1 средняя гармоническая;
при m = 0 средняя геометрическая;
при m = 1 средняя арифметическая;
при m = 2 средняя квадратическая;
при m = 3 средняя кубическая.

Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.

В чем состоит правило мажорантности средних?

Ответ

Мажорантность средних - состоит в том, что средняя некоторого вида всегда больше средней некоторого другого вида (для признака, не могущего иметь отрицательных значении).

Правило мажорантности средних величин

Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:

В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.

9.

Какова формула расчета среднего арифметического?

Какова формула расчета среднего арифметического взвешенного?

Какие свойства среднего арифметического Вам известны?

Где применяется среднее арифметическое? Приведите пример.

1. Средняя арифметическая

1.1 Средняя арифметическая простая.

При небольшом объёме исходной информации, когда исходные данные не сгруппированы, применяется средняя арифметическая простая,которая рассчитывается по формуле:

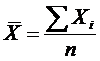
где ΣX_i- сумма значений;

n- число значений.

Например: В бригаде четверо рабочих в возрасте 21, 22, 23 и 24 года. Средний возраст рабочего бригады составляет

1.2 Средняя арифметическая взвешенная.

Когда исходные данные сгруппированы, то расчёт средней производится по

формуле средней арифметической взвешенной:

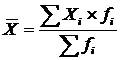
где f_i – частота ряда распределения, с которой отдельные варианты встречаются в совокупности (или удельный вес отдельных значений во всей совокупности).

Свойства средней арифметической:

1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты. Другими словами, постоянный множитель может быть вынесен за знак средней.

2. Если от каждой варианты отнять (прибавить) какое-либо произвольное число, то новая средняя уменьшится (увеличится) на то же число:

3. Если каждую варианту умножить (разделить) на какое-то произвольное число, то средняя арифметическая увеличится (уменьшится) во столько раз

4. Если все частоты (веса) разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится. Дело в том, что веса при исчислении средней арифметической выполняют роль удельного веса (соотношений между группами по количеству единиц). Поэтому замена частот частостями не меняет значения средней.

5. Сумма отклонений отдельных вариантов от средней арифметической всегда равняется нулю.

Перечисленные свойства могут быть использованы для того, чтобы облегчить технику исчисления средней арифметической.

Например. Можно из всех значений признака вычесть произвольную постоянную величину (лучше значение серединной варианты или варианты с наибольшей частотой), полученные разности сократить на общий множитель (лучше на величину интервала), а частоты выразить частостями (в процентах) и исчисленную среднюю умножить на общий множитель и прибавить произвольную постоянную величину. Иногда этот способ расчета средней арифметической также называется способом расчета от условного нуля. Широкое применение для обработки статистических материалов современных ЭВМ сужает необходимость исчисления средних по упрощенным схемам.

10.

Какова формула расчета среднего геометрического? Какова формула расчета среднего геометрического взвешенного? Где применяется среднее геометрическое? Приведите пример.

Среднегеометрическая величина дает возможность сохранять в неизменном виде не сумму, а произведение индивидуальных значений данной величины. Среднее геометрическое используют прежде всего тогда, когда среднее значение вычисляют для значений, заданных через некоторые равные промежутки времени (рост или снижение успеваемости, заработной платы, вклада в банке за несколько лет). Среднее геометрическое применяют тогда, когда переменная с течением времени изменяется примерно с одинаковым соотношением между измерениями. Среднее геометрическое применяют также тогда, когда отдельные значения в статистической совокупности удалены от других значений; это меньше влияет на среднее геометрическое по сравнению со средним арифметическим, а потому дает более правильное представление о среднем.

Среднегеометрические величины наиболее часто используются при анализе темпов роста экономических показателей.

Для расчетов средней геометрической простой используется формула:

Для определения средней геометрической взвешенной применяется формула:

11.

Какова формула расчета среднего гармонического? Какова формула расчета среднего гармонического взвешенного? Где применяется среднее гармоническое? Приведите пример.

Среднее гармоническое необходимо в том случае, когда наблюдения, для которых мы хотим получить среднее арифметическое, заданы обратными значениями.

Среднегармоническую величину можно определить по следующей формуле:

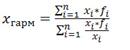
Среднегармоническую взвешенную величину можно определить по следующей формуле:

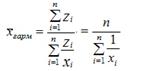
12.

Какова формула расчета среднего квадратического? Какова формула расчета среднего квадратического взвешенного? Где применяется среднее квадратическое? Приведите пример.

Среднее степенное второго порядка называют средним квадратичным, его используют при вычислении среднего квадратичного отклонения. Эти величины точно характеризуют изменение экономических показателей по сравнению с их базисной величиной, взятое в его усредненной величине.

Средняя квадратическая простая вычисляется по формуле:

Средняя квадратическая взвешенная равна:

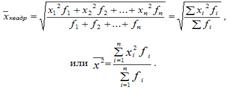
13.

Вариа́ция — различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени. Причиной возникновения вариации являются различные условия существования разных единиц совокупности. Вариация — необходимое условие существования и развития массовых явлений. Определение вариации необходимо при организации выборочного наблюдения, статистическом моделировании и планировании экспертных опросов. По степени вариации можно судить об однородности совокупности, устойчивости значений признака, типичности средней, о взаимосвязи между какими-либо признаками.

Показатели вариации

Абсолютные показатели

размах вариации:;		$\mathbf\R=x_{max} - x_{min}$
среднее линейное отклонение:;		$a=\frac{1}{n}\sum_{i=1}^n \|x_i-\bar{x}\|$
среднеквадратическое отклонение:;		$\quad \sigma=\sqrt{\frac{1}{n}\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}$
дисперсия:;		$\quad \sigma^2 = \frac{1}{n} \sum\limits_{i=1}^n \left(x_i - \bar{x} \right)^2$
среднее квартильное расстояние:.	$\mathbf\ q =\frac{(Q_3-Me)+(Me-Q_1)}{2}=\frac{(Q_3-Q_1)}{2}$

Относительные показатели

относительный размах вариации (коэффициент осцилляции):;		$\rho=\frac{R}{\bar{x}}$
относительное отклонение по модулю (линейный коэффициент вариации):;		$\ m =\frac{a}{\bar{x}}$
коэффициент вариации: где μ — математическое ожидание.		$\nu=\frac{\quad\sigma}{\bar{x}}$ $\nu = {\sigma \over \mu }$
Коэффициент вариации случайной величины — мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет ее средний разброс. В отличие от среднего квадратического или стандартного отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. Исчисляется в процентах. Вычисляется только для количественных данных.
· относительное квартильное расстояние:	$\ d =\frac{q}{\bar{x}}$

14.

Размах вариации

Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:

Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.

15.

Cреднее линейное отклонение

Cреднее линейное отклонение - это средний модуль отклонений значений X от среднего арифметического значения. Его можно рассчитывать по формуле средней арифметической простой - получим среднее линейное отклонение простое:

Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4. Рассчитаем среднее линейное отклонение простое: Л = (|3-4|+|4-4|+|4-4|+|5-4|)/4 = 0,5.

Если исходные данные X сгруппированы (имеются частоты f), то расчет среднего линейного отклонения выполняется по формуле средней арифметической взвешенной - получим среднее линейное отклонение взвешенное:

среднее линейное отклонение взвешенное

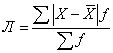
Вернемся к примеру про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4 и среднее линейное отклонение простое = 0,5. Рассчитаем среднее линейное отклонение взвешенное: Л = (|3-4|*1+|4-4|*2+|5-4|*1)/4 = 0,5.

16.

Как рассчитывается дисперсия признака (простое и взвешенное)? В чем измеряется этот показатель? Какие свойства выборки (амплитуда колебаний, степень колеблемости относительно средней, однородность) показывает этот показатель? Приведите пример.

Дисперсия признака (s²) определяется на основе квадратической степенной средней:

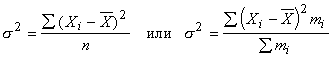простая взвешенная

Показатель s, равный , называется средним квадратическим отклонением.

В общей теории статистики показатель дисперсии является оценкой одноименного показателя теории вероятностей и (как сумма квадратов отклонений) оценкой дисперсии в математической статистике, что позволяет использовать положения этих теоретических дисциплин для анализа социально-экономических процессов.

Если вариация оценивается по небольшому числу наблюдений, взятых из неограниченной генеральной совокупности, то и среднее значение признака определяется с некоторой погрешностью. Расчетная величина дисперсии оказывается смещенной в сторону уменьшения. Для получения несмещенной оценки выборочную дисперсию, полученную по приведенным ранее формулам, надо умножить на величину n / (n - 1). В итоге при малом числе наблюдений (< 30) дисперсию признака рекомендуется вычислять по формуле

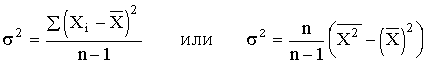Обычно уже при n > (15÷20) расхождение смещенной и несмещенной оценок становится несущественным. По этой же причине обычно не учитывают смещенность и в формуле сложения дисперсий.

Если из генеральной совокупности сделать несколько выборок и каждый раз при этом определять среднее значение признака, то возникает задача оценки колеблемости средних. Оценить дисперсию среднего значения можно и на основе всего одного выборочного наблюдения по формуле

где n – объем выборки; s² – дисперсия признака, рассчитанная по данным выборки.

Величина носит название средней ошибки выборки и является характеристикой отклонения выборочного среднего значения признака Х от его истинной средней величины. Показатель средней ошибки используется при оценке достоверности результатов выборочного наблюдения.

Показатели относительного рассеивания. Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.

1. Коэффициентом осцилляции отражает относительную колеблемость крайних значений признака вокруг средней

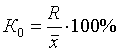2. Относительное линейное отключение характеризует долю усредненного значения признака абсолютных отклонений от средней величины

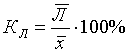3. Коэффициент вариации:

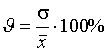
является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин.

В статистике совокупности, имеющие коэффициент вариации больше 30–35 %, принято считать неоднородными.

У такого способа оценки вариации есть и существенный недостаток. Действительно, пусть, например, исходная совокупность рабочих, имеющих средний стаж 15 лет, со средним квадратическим отклонением s = 10 лет, «состарилась» еще на 15 лет. Теперь = 30 лет, а среднеквадратическое отклонение по-прежнему равно 10. Совокупность, ранее бывшая неоднородной (10/15 × 100 = 66,7%), со временем оказывается, таким образом, вполне однородной (10/30 × 100 = 33,3 %).

17.

Как рассчитывается среднеквадратичное отклонение признака (простое и взвешенное)? В чем измеряется этот показатель? Какие свойства выборки (амплитуда колебаний, степень колеблемости относительно средней, однородность) показывает этот показатель? Приведите пример.

Среднее квадратичное отклонение определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из дисперсии и может быть найдена так:

1. Для первичного ряда:

Среднее квадратичное отклонение для первичного ряда

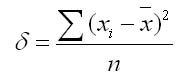
2. Для вариационного ряда:

Среднее квадратичное отклонение для вариационного ряда

Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:

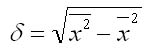
формула среднего квадратичного отклонения

Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.

Для альтернативных признаков формула среднего квадратичного отклонения выглядит так:

где р — доля единиц в совокупности, обладающих определенным признаком;
q — доля единиц, не обладающих этим признаком.

Среднее квадратическое

Среднее квадратическое применяется, например, для вычисления средней величины сторон n квадратных участков, средних диаметров стволов, труб и т. д. Она подразделяется на два вида.

Средняя квадратичная простая. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратичной средней величиной.

Она является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число: Средняя квадратичная взвешенная вычисляется по формуле:

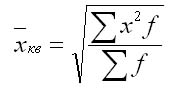
Средняя квадратичная взвешенная

где f — признак веса.

18.

Как рассчитывается показатель вариации (линейный и нелинейный)? В чем измеряется этот показатель? Какие свойства выборки (амплитуда колебаний, степень колеблемости относительно средней, однородность) показывает этот показатель? Приведите пример.

Чтобы дать представление о величине варьирующего признака недостаточно исчислить средний показатель. Кроме средней необходим показатель, характеризующий вариацию признака.

Вариация – это изменение значения признака у отдельных единиц совокупности. Вариация обусловлена действием различных факторов на развитие отдельных единиц совокупности. Чем более разнообразно условие, тем больше его вариация.

Наиболее простой характеристикой вариации признака является размах вариации (R). Размах вариации – это разность между наибольшим и наименьшим значением признака в изучаемой совокупности:

R=x_max-x_min,

где x_max – наибольшее значение признака;

x_min – наименьшее значение признака.

Размах вариации не отражает отклонений всех значений признака – это его недостаток. Он исчисляется при контроле качества продукции для определения систематически действующих причин на производственный процесс.

Для измерения отклонения каждой варианты от средней величины в ряду распределения или в группировке применяется среднее линейное отклонение (d).

Среднее линейное отклонение определяется по формулам:

а) для несгруппированных данных (ранжировочного ряда) (простое);

б) для вариационного интервального ряда: (взвешенное).

Среднее линейное отклонение показывает, на сколько в среднем каждое значение признака отклоняется от средней величины. Эта величина всегда именованная и измеряется в тех же величинах, в которых даны статистические показатели.

Среднее линейное отклонение дает обобщенную характеристику степени колеблемости признаков совокупности. Средние линейные отклонения применяются на практике для анализа состава рабочих, ритмичности производства, равномерности поставок материалов и т.д.

Наибольшее применение в практике статистических работ находит показатель – дисперсия признака или средний квадрат отклонений, или квадрат среднего квадратического отклонения (). Дисперсия – – определяется по формулам:

а) для ранжировочного ряда (несгруппировочных данных): (простая);

б) для интервального ряда: (взвешенная).

Корень квадратный из дисперсии представляет среднее квадратическое отклонение (): ; или

а) для ранжировочного ряда: (простое);

б) для вариационного ряда: (взвешенное).

Среднее квадратическое отклонение дает обобщенную характеристику признака совокупности и показывает во сколько раз в среднем колеблется величина признака совокупности. В зарубежной литературе оно называется стандартным отклонением и применяется в различных стандартах. Среднее квадратическое отклонение по величине всегда больше среднего линейного отклонения. Среднее квадратическое отклонение является мерой надежности средней величины: чем оно меньше, тем точнее средняя арифметическая.

Дисперсия является оценкой одноименного показателя теории вероятности. Сопоставление линейных или среднеквадратических отклонений по признакам совокупности дает возможность определить статистическую однородность совокупности: чем меньше размер, тем совокупность более однородна.